关于2025年度中国科学院杰出科技成就奖的
推荐公示
根据《中国科学院杰出科技成就奖条例》和《中国科学院杰出科技成就奖条例实施细则》（科发规字〔2024〕39号），拟推荐“周向宇”作为2025年度中国科学院杰出科技成就奖（个人奖）候选者，现按要求进行公示（详见附件）。
自公布之日起7个自然日为异议期。任何单位和个人对候选者的成果真实性、水平、创新性及贡献等如有异议，应以书面形式并实名向本单位提出。
以单位名义提出的异议，应在异议材料上加盖单位公章，签署法定代表人姓名，并写明联系人地址、电话和电子信箱。以个人名义提出的异议，应在异议材料上签署真实姓名，并写明本人工作单位、联系地址、电话和电子信箱。
凡表明真实身份、如实提出异议意见、提供必要证明材料的异议为有效异议。我们将对异议受理截止期前受理的有效异议进行核实处理，对异议提出者予以严格保密。
联 系 人：武晓棽
联系地址：北京市海淀区中关村东路55号南楼313
联系电话：010-82541770
E-mail：sci@amss.ac.cn
中国科学院数学与系统科学研究院
2025年10月9日
个人成就奖—周向宇
中国科学院数学与系统科学研究院
一、推荐意见（不超过300字）
多复变是现代数学所有学科中最深刻、最困难的理论之一。周向宇在多复变最前沿领域长期探索与积累，提出了自己的视角、思想与方法，解决了核心困难问题，做出了里程碑式的重大成就，开辟了一个全新的研究分支，引领了多复变跨学科发展。
周向宇证明了在苏联《数学百科全书》列为未解决问题的扩充未来光管猜想，被俄罗斯科学院院士评价为“帮助物理获得隐藏在公理后的新知识”，对Hilbert第六问题及规范场论千禧问题做出贡献；解决了最优L2延拓问题及Suita猜想，被Ohsawa称为“令人瞩目的成就”；证明了“被认为相当不可企及的”“复分析与位势论中核心问题”Demailly强开性猜想；建立了L2逆理论并解决Lempert问题；揭示了中国古代数学成就及其对华夏文明和现代数学的影响。
二、代表作列表
1. 周向宇. A proof of the extended future tube conjecture. Izvestiya RAN, Series Math. T.62, 211-224 (1998).
2. 周向宇. 中国古代数学的贡献. 数学学报(中文版), 2022, 65 (04): 581-598
3. 朱朗峰, 关启安, 周向宇. On the Ohsawa-Takegoshi L2 extension theorem and the Bochner-Kodaira identity with non-smooth twist factor. J. Math. Pures Appl. (9) 97 (2012), no. 6, 579-601.
4. 关启安, 周向宇. A solution of an L2 extension problem with an optimal estimate and applications. Ann. of Math. (2) 181 (2015), no. 3, 1139-1208.
5. 关启安, 周向宇. Effectiveness of Demailly's strong openness conjecture and related problems. Invent. Math. 202 (2015), no. 2, 635-676.
6. 关启安, 周向宇. A proof of Demailly's strong openness conjecture. Ann. of Math. (2) 182 (2015), no. 2, 605-616.
7. 关启安, 周向宇. Optimal constant in an L2 extension problem and a proof of a conjecture of Ohsawa. Sci. China Math. 58 (2015), no. 1, 35-59.
8. 周向宇, 朱朗峰. An optimal L2 extension theorem on weakly pseudoconvex Kähler manifolds. J. Differential Geom. 110 (2018), no. 1, 135-186.
9. 邓富声, 宁家福, 汪志威, 周向宇. Positivity of holomorphic vector bundles in terms of Lp-estimates of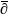 
. Math. Ann. 385 (2023), no. 1-2, 575-607.
10. 邓富声, 汪志威, 张利友, 周向宇. New characterization of plurisubharmonic functions and positivity of direct image sheaves. Amer. J. Math. 146 (2024), no. 3, 751-768.
附件下载：