非线性椭圆偏微分方程学术研讨会

2025年9月19日-9月22日

组织者：麻希南，邱国寰

联系人：邱国寰 qiugh@amss.ac.cn

题目和摘要:

1. 题目: Resolvent Estimates for the Stokes Operator in Bounded C^1 Domains

报告人：耿俊（兰州大学）

摘要: We establish resolvent estimates in L^q spaces for the Stokes operator in a bounded $C^1$ domain. As a corollary, it follows that the Stokes operator generates a bounded analytic semigroup in L^q for any 1<q<.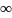

2. 题目：Convergence rates and regularity for multiscale elliptic homogenization

报告人：诸葛金平（中科院数学所）

摘要：I will talk about linear second-order elliptic equations with coefficients periodically oscillating at multiple different scales. The optimal convergence rates and uniform regularity will be discussed in different situations, particularly when the scale-separation condition is not satisfied. This is joint work with Weisheng Niu and Yao Xu.

3. 题目：Qualitative and quantitative Homogenization of Hamilton-Jacobi equations

报告人：荆文甲（清华大学）

摘要：Since the pioneering unpublished paper of P.L. Lions, Papanicolaou and Varadhan, homogenization problems for Hamilton-Jacobi equations in periodic or stationary ergodic environments, in viscous or inviscid settings, has received a lot of attention. These problems arise naturally in applications such as optimal control and combustion theory in heterogeneous environments. In this talk I shall first give a very brief overview of the topic and then focus on some recent results on optimal convergence rates in the periodic setting.

4. 题目: Resolvent Estimates for the Stokes Operator in Bounded C^1 Domains

报告人：涂绪山（香港科技大学）

摘要: In this talk, we study a Monge-Amp\`ere obstacle problem, which was initially studied by Savin, and discuss related topics. First, we develop regularity theory for $\det D^2u=u^q$, establish Liouville theorems for its entire solutions. Next, we develop a variational framework for Aleksandrov estimates of convex solutions, identifying both isolated singularity problems and obstacle problems as extremal configurations, and establish refined Alexandrov-Bakelman-Pucci (ABP) estimates under suitable assumptions. Furthermore, we present a global version of these improved ABP estimates and generalize a theorem of Caffarelli and Li. Finally, we may discuss the Monge-Amp\`ere equations with multiple isolated singularities, with particular emphasis on how obstacle problems influence their structural behavior. This is joint work with Tianling Jin and Jingang Xiong.

5. 题目：Local potential and Holder estimates for the linearized Monge-Ampere equation

报告人：周斌（北京大学）

摘要：We establish local potential estimate and Holder estimate for solutions of linearized Monge-Ampere equations with the right-hand side being a signed measure, under suitable assumptions on the data. In particular, we obtain a new proof for the Holder estimate of non-homogeneous linearized Monge-Ampere equation.

6. 题目：A General form of Newton-Maclaurin type inequalities

报告人：任长宇（吉林大学）

摘要：In this talk, I will introduce a general form of the Newton- Maclaurin type inequality. We have extended the Newton- Maclaurin inequality for elementary symmetric functions to the case of linear combinations of multiple elementary symmetric functions.

7. 题目：Monge-Ampere equations in convex polytopes

报告人：黄耿耿（复旦大学）

摘要：In this talk, we will talk about our recent regularity results of Monge-Ampere equations in convex polytopes with Dirichlet boundary condition. This is a joint work with Weiming Shen.

8. 题目：Entire solutions and asymptotic behavior to a class of Parabolic k-Hessian Equations

报告人：蒋飞达（东南大学）

摘要：In this talk, we make a systematic investigation of the existence, uniqueness and nonexistence of entire separable variable radial solutions to the following class of parabolic $k$-Hessian equations with the parameter $\alpha$:

1. $$-u_t[S_k(D^2u)]^\alpha = 1.$$

We also study the asymptotic behavior and its refined version of the solution at infinity. The main tools employed in this work comprise Euler's broken line method, local boundedness estimate, Keller-Osserman type criteria, the generalized L'Hospital's rule, and asymptotic stability analysis.

9. 题目: sigma_k Yamabe problem revisited

报告人：王国芳（弗莱堡大学）

摘要: In this talk we revisit the $\sigma_k$ Yamabe problem and prove the existence in a larger cone than the usual one and prove various geometric inequalities. The talk is based on a joint program with Yuxin Ge and Wei Wei.

10. 题目: Classification results of Liouville equations and rigidity of Riemannian surfaces

报告人：欧乾忠（云南师范大学）

摘要: We study the Liouville equation $\triangle u+e^{2u} =0$ in a Riemannian surface $(M, g)$ with nonnegative $Ricci$ curvature. Under some asymptotic lower bound assumptions, we classify all the solutions to this equation, meanwhile we obtain the rigidity results for the ambient manifold. Note that our assumptions are optimal in some sense and differ from the classical assumption of finite total curvature.

11. 题目：Second boundary value problem for Hessian curvature equations and curvature flows

报告人：王志张 （复旦大学）

摘要：In this paper, we establish the existence of strictly convex solutions to the k-Hessian curvature equations and curvature flow equations in Ω, subject to the second boundary condition Du(Ω) = Ω∗, where Ω and Ω∗ are smooth strictly convex bounded domains in R^n.

12. 题目：The Neumann problem of special Lagrangian type equations

报告人：张德凯 （华东师大）

摘要：The special Lagrangian equation is an fully nonlinear elliptic PDE, which arises from several important geometric problems. In this talk, we study the Neumann problem for special Lagrangian type equations with critical and supercritical phases. These equations naturally generalize the special Lagrangian equation and the k-Hessian equation. By establishing uniform a priori estimates up to the second order, we obtain the existence result. This is a joint work with Prof. Guohuan Qiu.