量子计算在组合优化领域具有重要应用潜力，但现有算法普遍面临解空间过大、硬件实现困难等挑战。数学所尚云研究员及其硕士生白旭峻针对经典NP难问题——旅行商问题（TSP），创新性地提出基于量子动态规划的搜索算法，首次实现了从𝑂((𝑁−1)!)到 𝑂(\sqrt((𝑁−1)!))的平方级加速。该工作即将发表于理论计算机科学权威期刊（Theoretical Computer Science）。

    旅行商问题（TSP）是组合优化领域中一个重要的NP难问题。量子搜索框架因其严格的理论保证而被考虑用于此问题的加速求解，但这需要从一个非常大的解空间中搜索出所有的哈密顿圈，极大地削弱了量子搜索算法的优势。为克服这一问题，可以先制备出所有可行解的叠加态，再从中放大最优解的振幅。本文工作基于量子动态规划提出了一个可在多项式门复杂度内制备哈密顿圈均匀叠加态的量子算法，相比基于搜索的初态制备方法实现了指数加速，从而可以将TSP转化为最小值查找问题并实现真正的二次加速，达到了求解一般TSP的量子搜索算法的理论最低查询复杂度。

    此工作设计的算法避免了传统量子搜索方法中复杂的初始态制备和高资源消耗，通过量子动态规划和简化QFT等技术，显著降低了量子比特需求和线路复杂度。实验结果表明，该算法在4至8节点TSP实例中可以达到很高的准确性，为量子计算在组合优化问题中的应用提供了新思路。该成果为物流优化等实际工程问题提供了启发性的量子解决方案，推动量子计算从理论向应用转化。

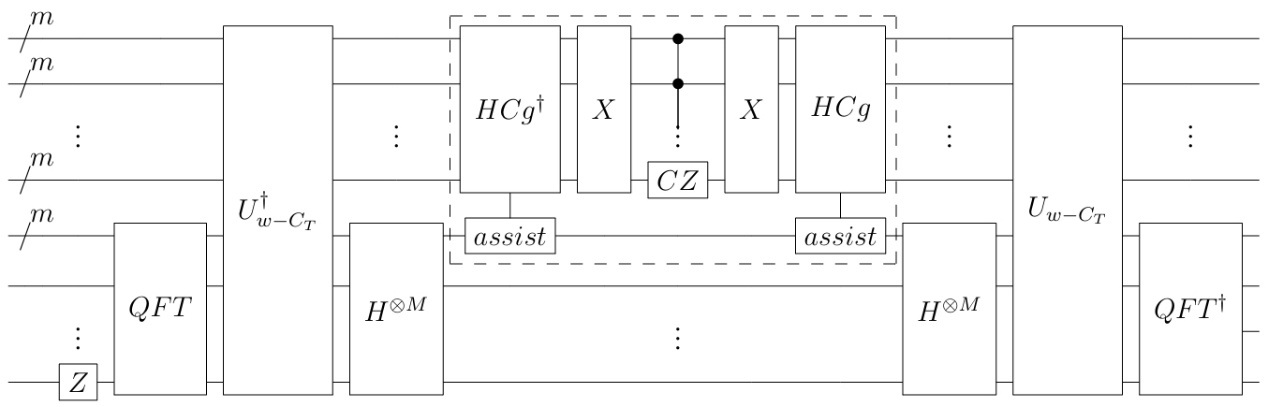
图1.算法主要框架的量子线路图

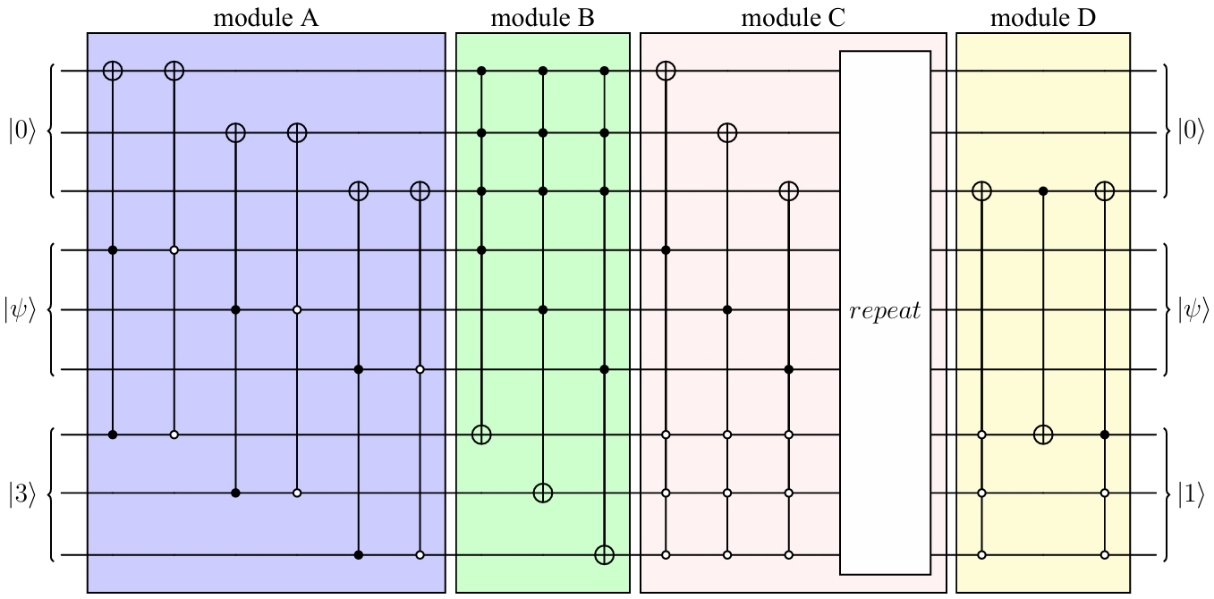
图2.初态制备/哈密顿圈生成算法的部分量子线路

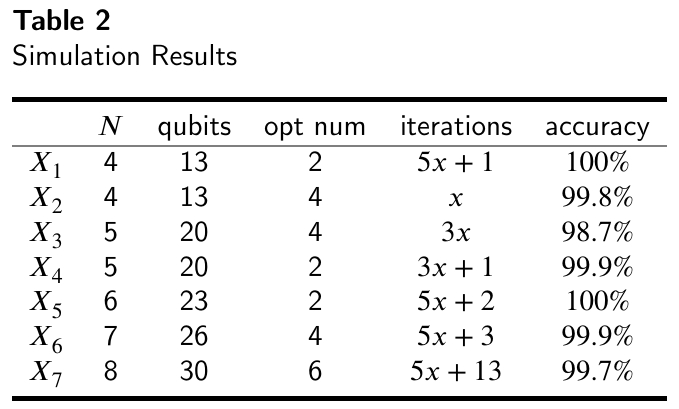
图3.算法在不同实例上的实验结果

图4.和已有量子搜索算法的比较

Publication:

Theoretical Computer Science, 2025

Author:

Xujun Bai

Academy of Mathematics and Systems Science, Chinese Academy of Sciences;

School of Mathematical Sciences, University of Chinese Academy of Science

Yun Shang

State Key Laboratory of Mathematical Sciences, Academy of Mathematics and Systems Science, Chinese Academy of Sciences

shangyun@amss.ac.cn (Corresponding author)