梯度流是一类以能量耗散为特征的偏微分方程，在众多领域处于核心地位。梯度流中通常含有复杂的非线性项。在数值方法层面，在精度、效率、实现简便等一般标准之外，对能量耗散的保持为梯度流数值求解的重要考量。

徐劼与合作者建立了标量辅助变量（scalar auxiliary variable，简称SAV）方法 [1,3] 处理梯度流中的非线性项。SAV 方法的基本假设为能量泛函中包含一个主导的非负二次项，剩余部分有下界。该假设是大多数有实际意义能量泛函所必需的条件，去掉了此前梯度流能量耗散格式对能量泛函形式的诸多限制。在设计数值格式时，首先对非线性项部分引入辅助标量，与辅助标量的演化方程共同构成等价系统；其能量泛函等价地表达为主导二次项与辅助标量项之和，称之为修正能量。在处理非线性项的时间离散时，只对辅助标量隐式处理。由此，可以得到线性隐式、修正能量无条件耗散、时间精度可达二阶的数值格式。SAV 方法的一大突出特点在于其求解非常方便，只需求解解耦的常系数线性方程。在诸多典型情形下，对应的常系数线性方程有快速算法，因而 SAV 方法的整体求解高效简便。

SAV 格式在多种不同特点的系统中都已证实其具有很好的效果。特别地，SAV 格式能够准确地把握复杂的有序结构，如准晶界面[4]（图）。

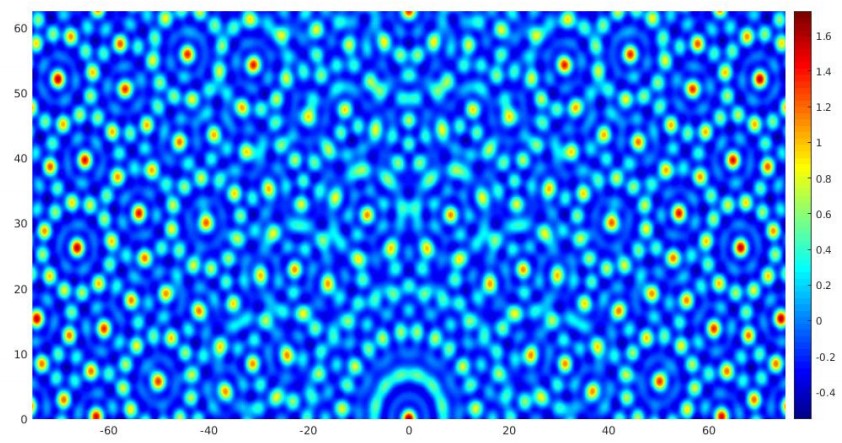
SAV 格式具有广泛适用性和灵活性。针对不同问题的特点，可以很方便对数值格式进行具体调整。一方面，辅助标量的数值格式结构还可用来处理零耗散项（如对流项），其他研究者针对其中的重要情形如 Navier-Stokes 方程、磁流体方程等做出了数值格式的相应发展。另一方面，基于辅助标量带来的简便求解性质，其他研究者将 SAV 格式推广到了任意高阶 Runge-Kutta 版本，以及引入了一般形式的标量 Lagrange 乘子力图更准确地保持梯度流的性质。上述推广中，前者需求解耦合的常系数线性方程，后者则需求解标量的非线性方程，在求解难度没有明显提升的情况下带来数值解更好的性质。

在收敛性和误差分析方面，SAV 格式的无条件能量耗散给数值分析开拓了发展空间。徐劼与沈捷教授合作，对于一大类典型的 L^2 和 H^{-1} 梯度流，在非线性项满足特定多项式增长的条件下，证明了 SAV 格式的收敛性并建立了误差估计 [2]。其中的关键在于从 SAV 格式的能量关系出发，导出数值解的 H^2 估计。这一结果突破了此前梯度流数值分析中通常采用的非线性项 Lipschitz 条件这一苛刻假定，为其它变形的辅助标量格式的分析提供了基本框架。

标量辅助变量方法的论文 [3] 获得了世界华人数学家联盟年会（ICCM 2024）的杰出论文奖（Distinguished Paper Award）和国际科学基础大会（ICBS 2025）的前沿科学奖（Frontiers of Science Award）（图）。

徐劼在2025年7月14日下午做前沿科学奖的获奖者报告（图）。

在报告中，徐劼分享了他提出辅助标量这一原创思想的过程。在沈捷教授的提议下，徐劼试图将此前已有的梯度流数值方法应用到液晶模型中，但因模型形式不符合数值方法的假定而无法推进。这促使徐劼去重新思考梯度流及其相关数值方法的结构。能量本身是一个标量，但此前都在函数层面处理，徐劼想到用辅助标量处理标量问题应该更为匹配。同时，徐劼敏锐地注意到了引入辅助标量后简便求解的途径、修正能量对函数的有效控制等关键要素，标量辅助变量方法得以最终成型。

近年来，徐劼与合作者还在有保持变量范围要求的梯度流数值格式方面取得了进展。其中针对 Poisson-Nernst-Planck 方程和 Keller-Segel 方程中保持区间 [5,6]、液晶单张量含拟熵项梯度流中保持张量特征值范围 [7]、双轴标架梯度流中的正交矩阵 [8] 几种不同情形的约束，发展了保持这些约束且能量耗散的数值方法。

相关论文

[1] Jie Shen, Jie Xu, Jiang Yang. The scalar auxiliary variable (SAV) approach for gradient flows, Journal of Computational Physics, 353, 407-416(2018).

[2] Jie Shen, Jie Xu. Convergence and error analysis for the scalar auxiliary variable (SAV) schemes to gradient flows, SIAM Journal on Numerical Analysis, 56(5), 2895-2912(2018).

[3] Jie Shen, Jie Xu, Jiang Yang. A new class of efficient and robust energy stable schemes for gradient flows, SIAM Review, 61(3), 474-506(2019).

[4] Duo Cao, Jie Shen, Jie Xu. Computing interface with quasiperiodicity, Journal of Computational Physics, 424, 109863(2021).

[5] Jie Shen, Jie Xu. Unconditionally bound preserving and energy dissipative schemes for a class of Keller-Segel equations, SIAM Journal on Numerical Analysis, 58(3), 1674-1695(2020).

[6] Jie Shen, Jie Xu. Unconditionally positivity preserving and energy dissipative schemes for Poisson--Nernst--Planck equations, Numerische Mathematik, 148, 671-697(2021).

[7] Yanli Wang, Jie Xu. Q-tensor gradient flow with quasi-entropy and discretizations preserving physical constraints, Journal of Scientific Computing, 94, 9(2023).

[8] Hanbin Wang, Jie Xu, Zhiguo Yang. A second-order SO(3)-preserving and energy-stable scheme for orthonormal frame gradient flow model of biaxial nematic liquid crystals, Journal of Scientific Computing, 99, 75(2024).